
by John P. Pratt
April 25, 2001
© 2001 by John P. Pratt. All rights Reserved.
| 1. Introduction |
| 2. Ecliptic vs. Sidereal |
| 3. Sidereal Coordinates |
| 4. Best-Fit Criteria |
| 5. The Solution |
| 6. Pi Vir |
| 7. Summary |
| Notes |
The star Pi Vir is proposed as the origin of sidereal longitude because 1) it is within .1° of the best centering point for the zodiac constellations, 2) it has longitudinal proper motion of only .01"/yr, 3) it is included in a line of three stars perpendicular to the ecliptic, and 4) it allows a simple definition for a uniform vernal equinox V which approximates the mean vernal equinox to ±.27° for the years -3400 to +4800: V= 210° -T/(72 yrs/° ), where T is the number of tropical years after the mean vernal equinox of the year 0.
Throughout history the construction of star maps has been plagued by the problem of precession of the equinoxes. Stars remain at nearly fixed positions relative to each other, but the celestial coordinates astronomers use are fixed to the earth rather than the sky, which causes coordinate lines to slowly drift among the stars. That is, because the origins of right ascension (equatorial coordinates) and of celestial longitude (ecliptic coordinates) are not located at a fixed point relative to the stars, but at the vernal equinox, the coordinates are continually changing. The same problem would occur with terrestial maps if the prime meridian were slowing drifting eastward from Greenwich, England by about 1°/72 years. In spite of this precessional drift, the traditional celestial maps are very useful because, after all, observations must be made from the earth. On the other hand, it is proposed that a coordinate system fixed to the stars could also be useful to both amateur and professional astronomers, as well as to historians and chronologists.
Constellations. One enduring celestial map which does not suffer from precession is the set of constellation figures. One specific star can often be singled out from the multitude by simply referring to its location in the figure, without need for numerical coordinates. When familiar with the constellations, the two words "Orion's sword" can be sufficient to locate the Great Nebula.
 |
Most modern celestial cartographers have apparently not recognized the value of the figures as a precise visual map. First, some details were overlooked, such as when the four streams of Aquarius were combined into one, which removed the ability to refer easily to any one of the twenty stars in the streams. Then the pictures were modified by whim, such as the location of Leo's hind feet, until the constellations were no longer standardized. Sometimes the artwork became so detailed as to obscure the stars, which was a hindrance rather than a help. Finally, deprived of their former utility, the figures were deemed to have no scientific value and were purged from most star atlases during the last century. They have not been deleted, however, from the amateur astronomer magazines because the figures are far more useful for explaining how to locate a planet. The coordinates which astronomers use are so clumsy as to be worthless to someone with a pair of binoculars. On the other hand, they are excellent for someone with a telescope on a permanent mount, with a computer-driven finding system.
"Stick figures" sometimes remain in celestial maps, but they are not standardized, they remove many of the stars from the recognition pattern, they often do not even remind one of the figure, and they often change the locations of stars in the figure. Many think of Regulus as the stick-figure lion's foot rather than the Lion's Heart. These shortcomings could, however, be corrected.
Fortunately, any scientific disdain for pictures that may have existed is now disappearing. Recent research shows the importance of visualization to recognizing interrelationships between complicated sets of data, such as a sky filled with stars. Not long ago many college texts were practically devoid of illustrations, but now pictures abound in texts and encyclopedias to utilize the picture-oriented right-half of the brain as well as the number-oriented left-half.
Best of Both Maps. This paper proposes that we should combine the best features of both coordinates and constellations. Some strengths and weakness of coordinates and constellations as maps are summarized in Table 1. Note that each is strong where the other is weak, which suggests combining the best features of each as follows.
| Coordinates | Constellations | |
| Strengths |
|
|
| Weaknesses |
|
|
1. Restore the constellation figures to star atlases, perhaps as an optional (overlay) feature, using standardized pictures. The classic Greek descriptions of Ptolemy (Taliaferro, 1952) and Aratus (Mair, 1960) could be used for historical consistency. Additional modern constellation figures could also be standardized to include most visible stars. The figures could be simple outlines printed in a pastel color that would not obscure any stars, but it would greatly enhance the usefulness of the atlas. "Stick figure" constellation drawings could also be standardized in a manner to help visualize the full figure. Lovi & Tirion (1989) have taken the first step toward restoring the constellation figures by publishing a modern star atlas combined with an old atlas that includes the figures. The next obvious step is to save the reader from having to turn pages back and forth between the two by simply superimposing the figures right over the modern star map.
2. Design "sidereal coordinates" around the constellations.The fixed ecliptic plane seems ideal to be the fundamental plane for sidereal coordinates because it is not affected by precession nor nutation and because the planets stay close to that plane. Longitude could be measured from a fixed star of low proper motion to eliminate the precession problem, and the origin could be chosen to approximately center the zodiac constellations so that the figures could help to visualize locations given by numerical coordinates. Although more than twelve constellations cross the ecliptic, and although they are of varying lengths, it would still be calculationally convenient to center the twelve classic figures into 30° sectors so that any sidereal longitude from 0-360° could be visualized easily by mentally dividing it by 30°.
Such sidereal coordinates, tailored to fit the zodiac constellations, could benefit the general skywatcher and the professional astronomer alike, as well as the researcher in history and chronology.
Both latitude and longitude on earth use the reference circle of the equator: latitude is measured in degrees north or south from it, and longitude is measured in degrees around it, starting from an arbitrary zero-point (in Greenwich, England). Similarly, the reference circle for ecliptic latitude and longitude is the ecliptic, which is the apparent path of the sun (and approximately of the moon and planets) through the stars. The zero-point of ecliptic longitude is the vernal equinox, which is the location of the sun on the ecliptic when it crosses into the northern half of the sky on the first day of spring. Unfortunately, that point slowly rotates or "precesses" around the ecliptic, causing all stars to increase in longitude by about 1° every 72 years.
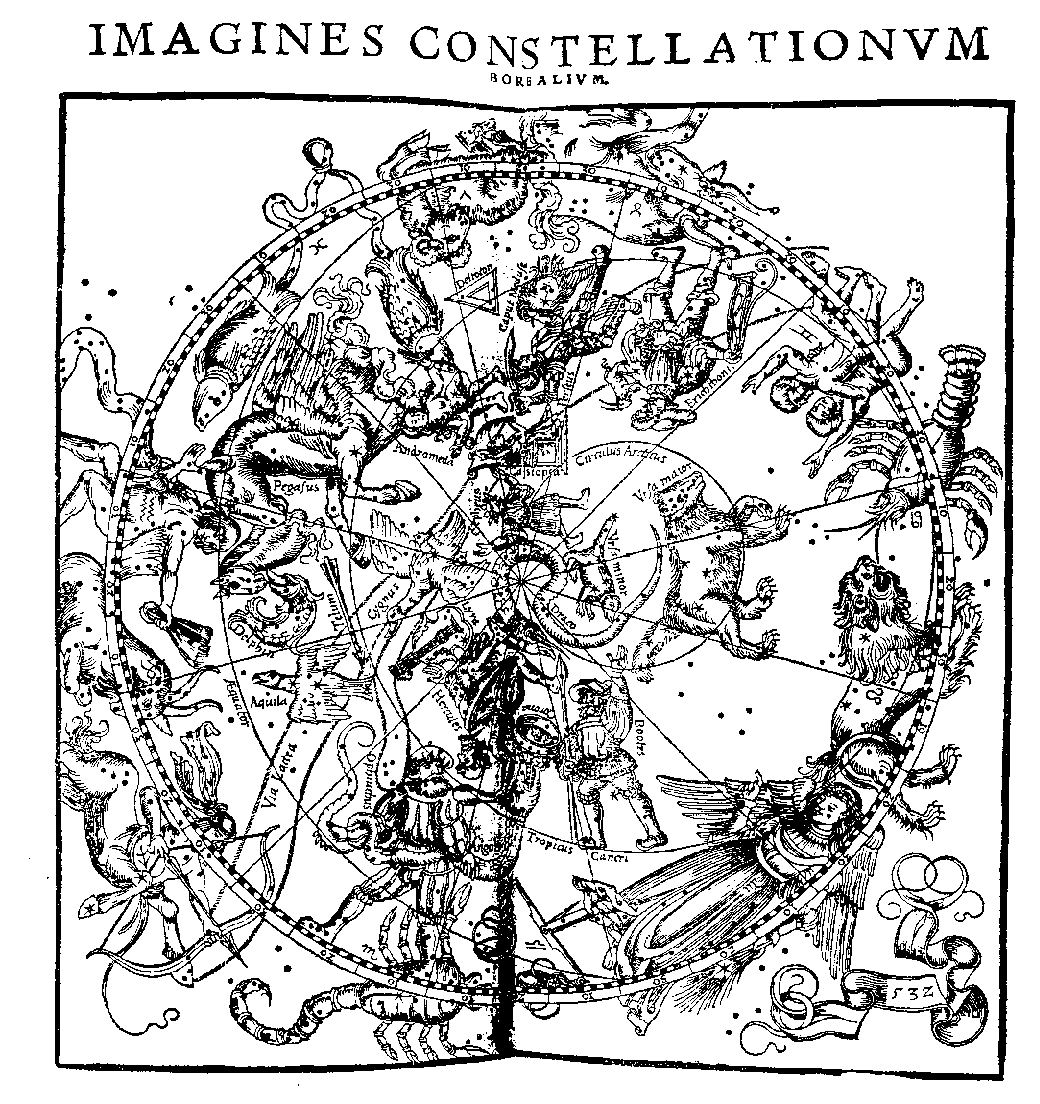 |
Star positions relative to the ecliptic plane are nearly fixed over the ages. The star positions in Fig. 1 were taken from Ptolemy's second century observations and the map was updated by simply precessing the vernal equinox. Thus, it is the coordinate lines, not the star positions, that date the map. This is not true of similar maps not centered on the ecliptic pole; when being updated they have to be entirely redrawn.
"Sidereal coordinates" solve the precession problem. Similar to ecliptic coordinates, they use the invariant (mean) ecliptic plane as the reference for "sidereal latitude," but the origin of "sidereal longitude" is a fixed star rather than the precessing vernal equinox.
After some uses of the new sidereal coordinates are discussed, a method will be proposed for selecting the best origin for sidereal longitude.
Visible Coordinates. Each zodiac constellation can be assigned to a 30° sector of sidereal longitude to facilitate visualizing positions. This is especially useful for mentally picturing the positions of planets given only their sidereal longitude. For example, a sidereal longitude of 275° can be mentally divided by 30° to get 5° into the tenth constellation. If familiar with sidereal coordinates, one can picture the location in Gemini, near Castor's left foot. Better yet, that longitude can be given simply as "5° Gem."
Thus, a monthly planetary calendar in popular astronomy magazines could include statements such as, "This month Mars stops at 26° Tau near the southern horn of Taurus and begins its retrograde motion," or "Uranus can be seen in binoculars at 14° Sag. near the head of Sagittarius."
Permanent Maps. Because the coordinate lines do not precess, maps and celestial spheres can be made that will not have to be updated for several hundred years, after which a few stars will have moved with their own "proper motion" about the width of the dot representing them. In fact, even that motion could be included on the map as a "trail" behind the star, thus making a truly permanent map. Sidereal longitude as well as the positions of the precessing equinoxes at various times could be indicated on the ecliptic circle, which is often devoid of marks in current atlases, such as Norton's 2000.0 (Ridpath, 1989).
The usual star-locator disks cannot be used for visualizing the sky of ancient Babylon because they use equatorial coordinates which suffer precessional drift. Planispheres and celestial spheres could be constructed using sidereal coordinates to show the constellations visible above the horizon at any time in history. They would have two axes of rotation, one centered on the ecliptic pole to select the desired year, and one centered on the celestial pole for the time of day.
History/Chronology. Sidereal longitude can be very useful for dating historical observations of the planets among the stars, such as those from ancient Babylon. The usual ecliptic longitude cannot be used to date such observations unless time consuming corrections are made for precession.
For example, a tablet from ancient Babylon gives dates on which the moon was near Pollux, Venus at Regulus and Mars at the Beehive Cluster (van der Waerden, 1974). The dates of these observations could be found by first converting the locations to the sidereal longitudes of 26° Gem, 3° Leo, and 10° Cnc with a table or on a planisphere star-locator. Note that either would be correct for all recorded history because the coordinates do not precess. Then the observation dates could be found by computer or tables that output the desired planetary positions directly as 26° Gem, 3° Leo, and 10° Can respectively. All the extra work of measuring longitude from the vernal equinox and then having to correct for its precession is eliminated.
As another example, sidereal coordinates might have sped up research on the "Star of Bethlehem" by several years. A prime candidate is the Venus/Jupiter conjunction on June 17, 2 B.C. (Sinnott 1968, Pratt 1990), which was discovered by searching tables of planetary longitudes. The Jupiter/Regulus triple conjunction that same year awaited eight more years to be discovered (Martin, 1976). If the tables had also listed sidereal longitudes, then Jupiter's triple crossing of Regulus at about "3° Leo" would have been obvious.
Calendars. Some civilizations measured time by use of sidereal calendars. For example, the Egyptian New Year's Day was at the heliacal rising of Sirius, and the Mayan Calendar incorporated planetary calendars. These can be studied more easily with sidereal coordinates.
Uniform Vernal Equinox. The precession of the vernal equinox has been used historically to mark ages of time. Sidereal coordinates can provide a framework in which to visualize the precession as well as to define a uniformly moving vernal equinox that could be useful both for approximating the true equinox and as a basis for reckoning time.
Rapid Computing. Many computer programs displaying stars graphically can run faster and be less subject to error using stellar data bases in sidereal coordinates because no precession calculations are required for some displays including only stars and planets.
Space Telescopes. Because it is the earth that precesses, space telescopes on inertial platforms could use sidereal coordinates which would not require any precession at all. If such had been used in the Hubble Space Telescope, the astronomical community could have avoided the nationally publicized embarrassment of having precessed the 1950.0 coordinates in the wrong direction.
Given that sidereal coordinates can be useful, the rest of this article discusses how to select the zero-point of longitude so that each zodiac constellation fits into its 30° sector as well as possible.
Fitting the zodiac constellations into 30° sectors is not trivial because they vary in length from 47° (Virgo) to 14° (Cancer). Moreover, some of them overlap the same portions of the ecliptic. Even though the long constellations cannot be squeezed into a 30° sector, a "best fit" is desirable anyway to have the calculational feature of 30° per constellation.
Definitions. The following terms are helpful to define best-fit criteria.
Constellation. To provide historical consistency, Ptolemy's star catalog (1952) is used to determine where the twelve zodiac constellations begin and end.
Sector Longitude. Longitude measured from the beginning of a 30° sector is called "sector longitude." This definition refers to either sidereal longitude or the usual ecliptic longitude measured from the vernal equinox. For example, a longitude of 307° corresponds to a sector longitude of 7° in either system.
The principal use of sector longitude in the new system will be for visualizing positions, as in the example of "5° Gem" given above. In this article, sector longitude from the 2000.0 vernal equinox will also be used to select an origin for sidereal longitude because stars with the same sector longitude are a multiple of 30° apart and hence could serve as visible sector boundary markers using the same origin.
Fit. "Fit" is defined as follows so that both long and short constellations might have an equal chance to fit into a sector. A constellation of less than 30° length fits into its sector if it is entirely contained in that sector; one of more than 30° length fits if it entirely covers its sector.
Corrected length. When two constellations share the same portion of the ecliptic, the overlapping region is considered part of the shorter constellation. Thus, for all calculations of fitting or centering, the length of the longer constellation is "corrected" by subtracting off the amount of overlap.
Using the above definitions, the following criteria were chosen to determine the origin of sidereal longitude. They are listed in order of priority.
Criterion 1. The zodiac constellations should each fit into its sector as well as possible. The origin must a) allow a maximum number of constellations to each fit into a sector, and then b) center them in those sectors as well as possible.
Criterion 2. Visible stars should mark the origin and sector boundaries where possible. This requirement is to facilitate visualization of the coordinates; so it is best if the origin is a) near the ecliptic, b) bright, c) in a line of stars perpendicular to the ecliptic, and d) of low proper motion so that it is a "fixed" star. A longitudinal proper motion of .01"/yr would cause a displacement of only .01° throughout recorded history (about 3,600 years).
Criterion 3. The origin should have symbolic significance. The origin should a) begin a constellation with a reasonable claim to head the zodiac, and if possible, b) be positioned at a key location in the constellation figure.
Criterion 4. The origin should allow a simple definition of a "uniform vernal equinox," which would move at a constant velocity along the ecliptic, approximating the accelerating mean vernal equinox throughout historical times.
The foregoing criteria were used to select an origin for sidereal longitude as follows. Table 2 lists for each constellation the 2000.0 longitude and location in the figure of its beginning and ending stars, and both the total and the corrected constellation lengths. The data in the table are derived from Hirshfeld and Sinnott (1982). First, each of the criteria is discussed in order of priority and then an overall rating independent of priority is calculated.
| Name | Begins | Pos. | 2000.0 Lon. | Ends | Pos. | 2000.0 Lon. | Total Length | Corrected Length |
| Vir | Xi Vir | Head | 173.34 | Mu Vir | Foot | 220.13 | 47 | 45 |
| Lib | Mu Lib | Claw | 224.17 | Theta Lib | Claw | 239.87 | 16 | 16 |
| Sco | Del Sco | Head | 242.57 | Iota Sco | Tail | 267.52 | 25 | 25 |
| Sgr | Gam Sgr | Point | 271.26 | 62 Sgr | Tail | 297.07 | 26 | 26 |
| Cap | Xi Cap | Horn | 302.49 | Mu Cap | Tail | 325.83 | 23 | 23 |
| Aqr | Eps Aqr | Strap | 311.72 | 108 Aqr | Stream | 350.30 | 39 | 24 |
| Psc | Beta Psc | Head | 348.58 | Alp Psc | Knot | 29.38 | 41 | 39 |
| Ari | Gam Ari | Horn | 33.18 | Tau Ari | Tail | 53.40 | 20 | 20 |
| Tau | Omi Tau | Side | 51.16 | Zeta Tau | Horn | 84.78 | 34 | 31 |
| Gem | Eta Gem | Foot | 93.44 | Kap Gem | Shoulder | 113.67 | 20 | 20 |
| Cnc | Mu Cnc | Foot | 119.48 | Alp Cnc | Claw | 133.64 | 14 | 14 |
| Leo | Kap Leo | Nose | 135.30 | Ups Leo | Feet | 175.04 | 40 | 40 |
Best-fit Range. Using the data in Table 2, it is calculated that the maximum number of constellations that can simultaneously fit into separate sectors is eight, with none of the other four failing by more than 3°. This best fit occurs when the origin has a 2000.0 sector longitude in a "best-fit range" of 27.52-29.38°. These endpoints are determined by Iota Sco, allowing Scorpius to fit in its sector, and Alpha Psc, allowing Pisces to cover its sector. The number that fit decreases to six for longitudes less than .5° before this range (27.07°, the end of Sgr) and only .1° afterit (29.48°, the beginning of Cnc).
Note that the best fit range is a set of twelve areas spaced every 30° around the ecliptic and that the origin could be chosen in any one of them.
Centering. The origin which would best center the I.A.U. zodiac constellations in their sectors would have a 2000.0 sector longitude of 27.1°, as determined by simply averaging the 2000.0 sector longitudes of the twelve boundary points (counting Ophiuchus as part of Scorpius). If the classical Ptolemaic definitions of the constellation boundaries are used, counting shared portions of the ecliptic as part of the shorter constellation, the best origin would be at 27.4°. That these results agree so closely is not surprising because the I.A.U. based its boundaries on the classical definitions. Probably the best center point to use would be slightly above 27.52°, which would allow all of Scorpius' tail to fit in its sector.
Visible Coordinates. A list of candidates for origin will now be made by checking each
potential sector boundary for any visible stars near the ecliptic and also near 27.5° longitude.
Other nearby stellar boundary markers will also be noted, including a few well placed dim stars.
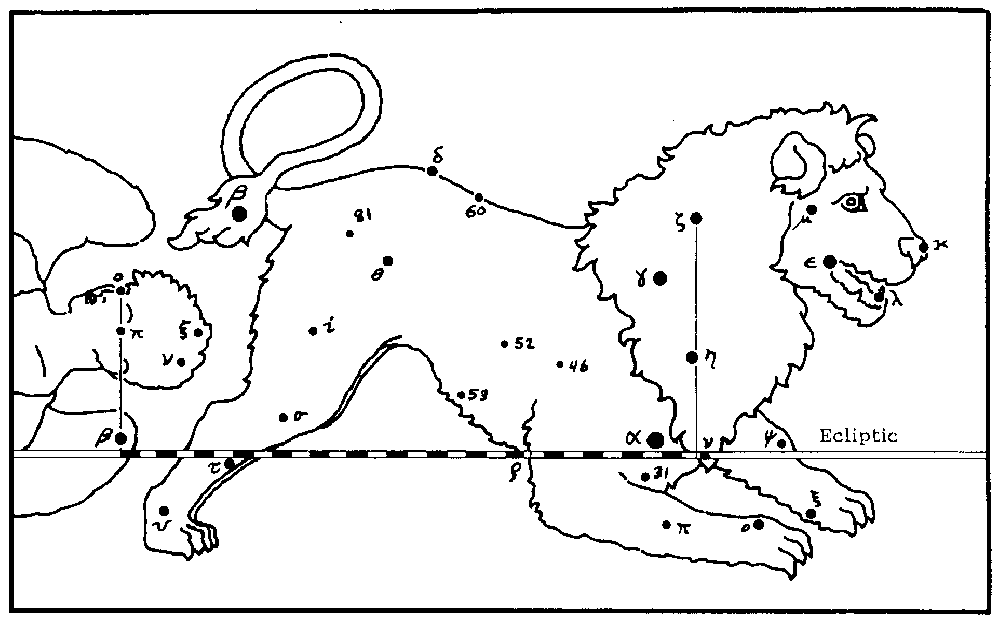 |
1. Virgo. The tip of Virgo's left wing (Beta Vir) is an excellent marker, being very near the ecliptic. It is enhanced by the two stars in her face (Pi and Omicron Vir), forming a straight line nearly perpendicular to the ecliptic (see Fig. 2).
2. Libra. This sector begins about 4° past Spica, but is otherwise unmarked.
3. Scorpius. The star Kappa Lib lies almost on the ecliptic and marks the beginning of the sector. The end is marked by the scorpion's tail (Iota Sco).
4. Sagittarius. The arrowhead (Gamma Sgr) is about 4° from the beginning of the sector and the end is marked by a line from 61 Sgr to 62 Sgr.
5. Capricornus. The right horn (Alpha and Beta Cap) forms a perpendicular to the ecliptic about 6° into the sector. Delta Cap in the tail is about 4° from the end.
6. Aquarius. The star Iota Aqr makes a good beginning boundary marker.
7. Pisces. This sector begins at the back of the western fish (Iota Psc). It ends with the perpendicular to the ecliptic formed by four stars in the eastern cord (Omicron, Pi, Eta, and Rho Psc). This cord is very conveniently placed because it is a clear marker in a bleak part of the sky.
8. Aries. The sector boundaries are those of Pisces and Taurus.
9. Taurus. This sector is easily visualized because the 25° span from the Pleiades to the tip of the southern horn (Zeta Tau) is centered.
10. Gemini. Gemini's 20° span is nearly centered in its sector. It begins with a perpendicular formed by the front star in Orion's club (Chi1 Ori), and 136 Tau. The sector ends about 4° past the perpendicular formed by the head of Pollux (Beta Gem) and his right shoulder (Kappa Gem).
11. Cancer. The boundaries are those of Gemini and Leo on either side. The sidereal sector boundaries of Leo and Virgo are each marked by a three-star line nearly perpendicular to the ecliptic. The two lines are separated by exactly 30°. All 27 stars in Leo listed by Ptolemy are shown as he described.
12. Leo. Two of the "sickle" stars in the neck (Zeta and Eta Leo) form a perpendicular with a dim star in the chest (Nu Leo) on the ecliptic that marks the sector's beginning. Moreover, the bright Regulus (Alpha Leo), within .5° of the ecliptic lies some 2° beyond the boundary, so this sector is very well marked.
Thus, Virgo and Leo are the best marked sectors, each having a 3-star perpendicular to the ecliptic, with Virgo having an easily visible star nearly on the ecliptic and Leo with two such stars farther away (See Fig. 3). Moreover, two of the stars in the perpendiculars (Pi Vir and Zeta Leo) are separated by almost exactly 30° of longitude. Pisces has a 4-star perpendicular, but only two of the stars are brighter than fifth magnitude. Conveniently, this perpendicular is also a multiple of 30° away from those of Virgo and Leo.
Heading the Zodiac. Taurus and Leo probably have the strongest historical claims for heading the zodiac because they first contained the spring equinox and summer solstice, respectively. Such claims, however, are temporary because of precession. Since the zodiac was first used, all twelve of the constellations have contained one of the equinoxes or solstices, so another criterion is needed.
Size and brightness often indicate importance. Not only would the first constellation be important, but also the last, which can be even greater than the first, like the anchor-man in a relay. Virgo and Leo are greatest in this respect, having the two longest corrected lengths and also containing bright stars. This reasoning suggests that Virgo is first and Leo is last because the order is specified by the motion of the sun and moon through the zodiac.
The choice of Virgo to head the zodiac has historical support. The ancient Greeks understood the sphinx to be the head of Virgo on the body of Leo (Allen, 1963), suggesting that Virgo "heads," or begins, the zodiac and that Leo is the "tail end." The symbolism of the head meaning first is widespread; for example, the Hebrew New Year's Day is called Rosh Hashanah, meaning "head of the year."
Anciently, Leo ruled over the constellations. In Men, Monsters and the Modern Universe (Lovi and Tirion, 1989), which combines a modern star atlas with the classic constellation figures, it is noted that, "Being the so-called 'King of Beasts,' the Lion was originally placed in this exalted position at the zodiac's highest location." Leo could be counted as the last and hence greatest of the constellations, even as the number 12 dominates the face of a clock at its highest location.
This comparison of the zodiac to the numbers on a clock is useful to remember the order of the constellations. Associate each of the "royal" constellations with a number on the face of a clock: Scorpius is 3, Aquarius is 6, Taurus is 9, and Leo is the king, being the 12. Then the others are easy to insert.
The sun, moon and planets move clockwise around the face of this "star clock," so they could be used as hands to measure time. For example, a new astronomical clock has recently been erected at Leicester University, England with the sun and moon each represented on the hands on a clock face showing the zodiac on the face (Mills, 1990). Thus, the clock analogy is best if "King Leo" is the 12, which means that Virgo is the 1.
In summary, Virgo has the strongest claim to head the zodiac because it puts the four royal constellations in the 3, 6, 9, 12 positions, with Leo at 12. Moreover, the Greeks taught that the whole point of the Sphinx is to tell us that the zodiac is headed by Virgo and ended by Leo. If a star other than one at the beginning of Virgo is chosen, it would probably be best to define sidereal longitude to begin at the appropriate multiple of 30°. For example, if a star in the eastern cord of Pisces is chosen, it could be defined to have longitude 210°.
Location in the Figure. The best location for a boundary star in a constellation would probably be at an extremity such as a head or horn, foot or claw, tail or rump. The worst would probably be a star not included by Ptolemy as part of the constellation.
Pi and Omicron Vir in Virgo's face have the strongest claims to be the origin based on position in the figure because they are in the head of the head constellation. The stars in the eastern cord of Pisces are also strong contenders because the cord is a prominent feature of the figure itself that forms a natural marker.
Uniform Vernal Equinox. Calculating the position of the vernal equinox throughout history suggests that the best natural marker is the eastern cord of Pisces, which was crossed by the equinox very near the year 0 (1 B.C.). Because it already forms part of the set of four natural boundaries discussed above, it would be calculationally convenient to use those boundaries because the uniform vernal equinox could be defined to be at 0° Aries in the year 0.
The mean vernal equinox is slowly accelerating: it currently moves along the ecliptic at 50.29" per year, but in the year -1000 its rate was 49.62"/year (Allen, 1976). Thus, a convenient and accurate uniform rate of precession over historical times can be defined to be exactly 50"/year (1°/72 years). This choice has the feature that it is an integer both in seconds per year and in years per degree.
As an example of using the cord of Pisces and the 72 yr/° rate, note that in Figure 1 the vernal equinox is about 9° before the cord, corresponding to the year -9° x 72 yr/° = -648. It is clearly a mistake in the woodcut, which purports to show the constellations for A.D. 1532 (complete with the latest garb). The intent must have been to show the equinox at the next sector boundary in Pisces, corresponding approximately to the year +21° x 72 yr/° = 1512.
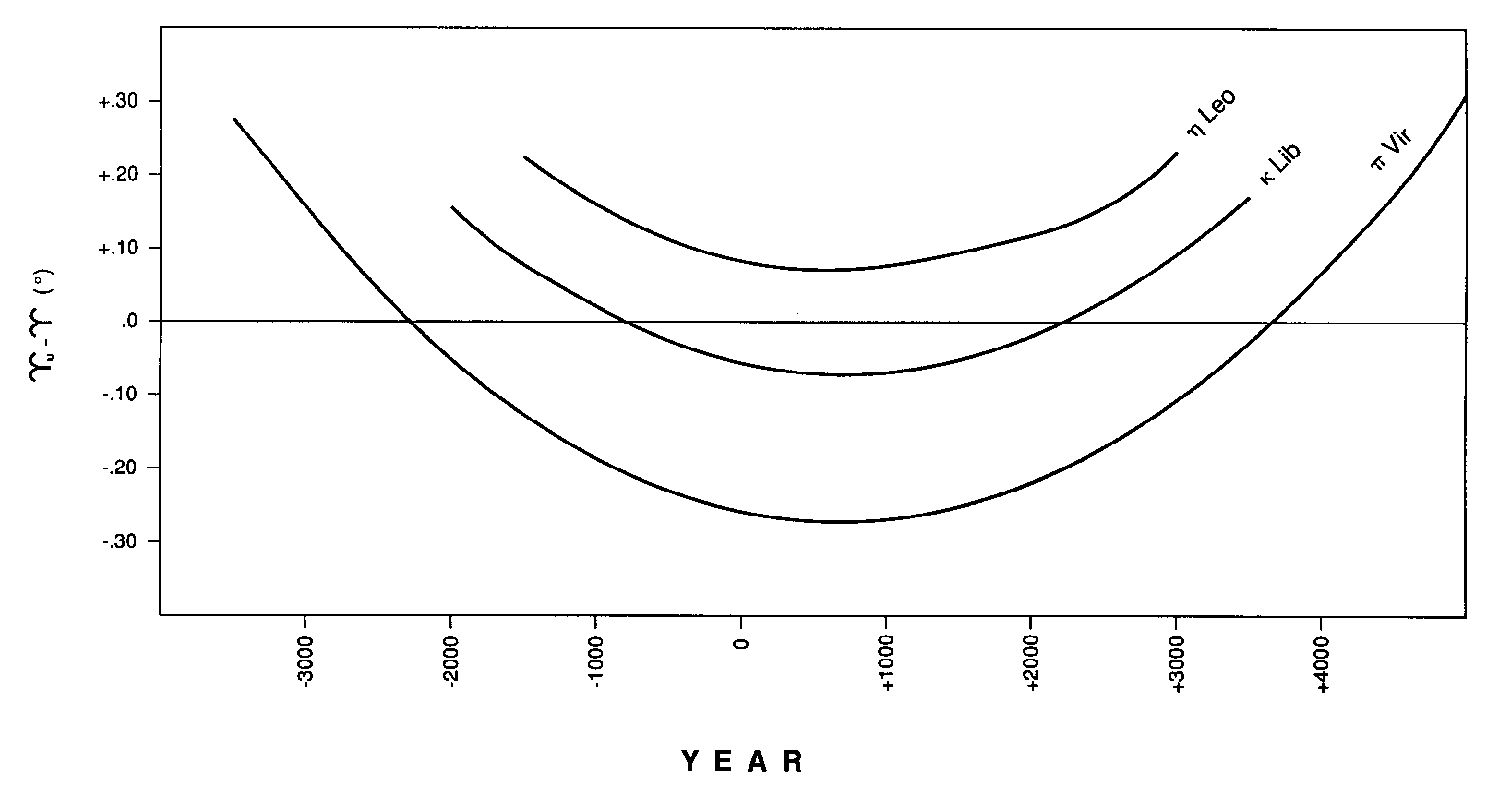
Combining this average rate with the position of a uniform equinox Vu at 0° Aries (= 30° Psc) at the mean equinox of the year 0 would lead to a very simple equation Vu = 30° Psc - T/(72 yr/°), where T is measured in tropical years from that time. How well this equation approximates the position of the mean vernal equinox depends on the position of 0° Aries, and hence on the choice of the origin. Figure 3 compares three low-proper-motion candidates for origin which best fulfill this requirement. It is seen that Kappa Lib would be the best choice for "short term" precessional effects because it approximates the mean equinox to within ±.07° for the period 1400 to +2800, and is currently within .02°. While Eta Leo could also be used as a short term choice, it suffers from never being more accurate than .07°. On the other hand, the choice of either Eta Leo or Pi Vir seems acceptable for longer terms because they stay within a maximum error of only ±.27° throughout the period -3400 to +4800.
 |
Overall Rating. Table 3 lists the boundary stars discussed and includes all possible candidates for origin with magnitude 4.8 or brighter, 2000.0 sector longitudes of 26.7-28.7°, and within 12° of the ecliptic, as well as a few other well-placed stars. In order to compensate for any undue dependence on the priorities assigned to the criteria, an overall rating is also included in Table 2 that is independent of priority. It is not intended as a final determination because sometimes only one serious weakness is enough to disqualify a candidate, such as the very high proper motion of the otherwise impressive Beta Vir.
| Star | Sec. Lon. | Fit | Lat. | Mag. | Line | PMlon | Con. | Loc. | Vu | Rating |
| Criterion: | 1 | 2a | 2b | 2c | 2d | 3a | 3b | 4 | Total | |
| Eta Psc | 26.82 | -.7 | 5.38 | 3.6 | 2 | .03 | Ari | Cord | 0 | 8 |
| Pi Psc | 26.91 | -.6 | 1.90 | 5.6 | 2 | -.05 | Ari | Cord | 0 | 7 |
| Gam Hyd | 27.02 | -.5 | -13.74 | 3.0 | 1 | -.09 | Lib | Tail | 0 | 6 |
| 85 Gem | 27.05 | -.5 | -0.88 | 5.4 | 0 | -.01 | Cnc | None | 0 | 5 |
| 62 Sgr | 27.07 | -.4 | -7.11 | 4.6 | 0 | .04 | Cap | Tail | 0 | 5 |
| Rho Psc | 27.08 | -.4 | 9.39 | 5.4 | 2 | -.02 | Ari | Cord | 0 | 6 |
| Beta Vir | 27.16 | -.4 | 0.69 | 3.6 | 2 | .78 | Vir | Wing | 0 | 10 |
| Chi Gem | 27.24 | -.3 | 7.23 | 4.9 | 0 | -.02 | Cnc | None | 0 | 3 |
| 3 Sgr | 27.24 | -.3 | -4.42 | 4.6 | 1 | -.00 | Sgr | None | 0 | 6 |
| Nu Leo | 27.34 | -.2 | 0.05 | 5.3 | 2 | -.02 | Leo | Chest | 1 | 10 |
| Eta Lib | 27.35 | -.2 | 4.00 | 5.4 | 1 | -.01 | Sco | None | 1 | 8 |
| Iota1 Sco | 27.52 | .0 | -16.71 | 3.0 | 1 | .00 | Sgr | Tail | 2 | 11 |
| Pi Vir | 27.56 | .0 | 6.15 | 4.7 | 2 | .01 | Vir | Head | 2 | 14 |
| Zeta Leo | 27.57 | .0 | 11.86 | 3.4 | 2 | .02 | Leo | Neck | 2 | 11 |
| Iota Psc | 27.64 | .1 | 7.15 | 4.1 | 2 | .17 | Psc | Back | 2 | 8 |
| Omi Vir | 27.69 | .2 | 8.52 | 4.1 | 2 | -.22 | Vir | Head | 2 | 11 |
| Omi Psc | 27.74 | .2 | -1.62 | 4.3 | 2 | .09 | Ari | Cord | 2 | 11 |
| Tau Vir | 27.75 | .2 | 13.06 | 4.3 | 1 | .02 | Lib | None | 2 | 7 |
| Kap Lib | 27.76 | .2 | -0.02 | 4.7 | 1 | -.02 | Sco | None | 2 | 10 |
| 13 Tau | 27.85 | .3 | 0.02 | 5.5 | 2 | -.00 | Tau | None | 2 | 10 |
| Eta Leo | 27.90 | .4 | 4.87 | 3.5 | 2 | .00 | Leo | Neck | 2 | 12 |
| 25 Aqu | 27.95 | .4 | 15.34 | 5.1 | 1 | -.06 | Aqr | Head | 2 | 7 |
| 30 Psc | 28.05 | .5 | -5.71 | 4.4 | 2 | .03 | Psc | None | 1 | 7 |
| 42 Lib | 28.32 | .8 | -4.14 | 5.0 | 1 | -.01 | Sco | None | 0 | 5 |
| 61 Sgr | 28.44 | .9 | 5.08 | 5.0 | 0 | -.01 | Cap | Wing | 0 | 4 |
| 136 Tau | 28.52 | 1.0 | 4.18 | 4.6 | 2 | -.00 | Gem | None | 0 | 6 |
| Ups Lib | 28.61 | 1.1 | -8.51 | 3.6 | 1 | -.01 | Sco | None | 0 | 6 |
| Chi1 Ori | 28.68 | 1.2 | -3.16 | 4.4 | 2 | -.18 | Gem | Club | 0 | 5 |
| Iota Aqr | 28.72 | 1.2 | -2.08 | 4.3 | 1 | .02 | Aqr | Rump | 0 | 8 |
| Alp Ori | 28.75 | 1.2 | -16.03 | 0.5 | 2 | .03 | Gem | Shldr | 0 | 6 |
The data in Table 3 (from Hirshfeld and Sinnott, 1982) for each criterion are divided into three categories: good (boldface and underlined print), fair (boldface) and poor (normal print). These categories either indicate natural separations in the data or divide the candidates roughly into thirds. The visible boundary is rated "good" if it contains 2 stars brighter than magnitude 4.5, one of them being within 6° of the ecliptic; "poor" if no boundary star is that bright, and "fair" otherwise. The constellation is rated "good" if Virgo, "fair" if one of four royals, or "poor" otherwise. The overall rating is calculated by counting 2 for each good, 1 for each fair, and 0 for each poor rating.
The candidate which best fulfills the criteria for the origin of sidereal longitude, both in order of priority and in the overall rating, is Pi Vir.
Best-fit Criteria. Unless disqualified by other criteria, the choice of origin should be the first star in the best-fit range (1a) because it also best centers the figures (1b). From Table 3, that star is Pi Vir. It is clearly a strong contender because it is part of a 3-star perpendicular (2c), has low longitudinal proper motion (2d), marks the beginning of Virgo (3a), and is even in Virgo's head (3b).
Pi Vir has no "poor" ratings, however, it is only "fair" in nearness to the ecliptic (2a) and brightness (2b). Even these average qualities are so enhanced by its excellent location between two brighter stars in a perpendicular to the ecliptic, that it is virtually ideal.
Overall rating. The candidate which best fulfills the criteria for the origin of sidereal longitude is Pi Vir, with the highest rating of 14 out of 16 possible. Checking the runners-up shows that most have a serious weakness: Beta Vir, Omicron Vir and Omicron Psc have high proper motion; Nu Leo and 13 Tau are dim, and Zeta Leo and Iota Sco far from the ecliptic. Eta Leo is the only serious challenger, being the only other candidate with no "poor" ratings. Its main advantage is brightness, but that is not enough to outweigh the alignment of Pi Vir with Beta Vir, so close to the ecliptic. Choosing Eta Leo would only result in an unwarranted decrease in centering, such as forcing Zeta Leo into Cancer's sector, as well as decreasing the long term accuracy of the uniform equinox. The only stars which could simplify that equation to be Vu = -T/(72 yr/°), would be in the eastern cord of Pisces, but none of those stars is acceptable: Eta, Pi, and Rho would give errors of at least .74° and Omicron has high proper motion. Thus Pi Vir is proposed as the best origin of sidereal longitude.
The case for Pi Vir is so strong that it could have been chosen from Criterion 2 alone. Of 21 3-star perpendiculars to the ecliptic, there are three that have all of their stars within the same 1.1° of sector longitude (the ten stars with 3 or 4 in Table 3). That means those three lines are not only very close to collinear and perpendicular to the ecliptic, they also happen to be spaced almost exactly 30° apart. Such a coincidence virtually requires that they be sector boundaries. Selecting one of them as origin that is near the average of their sector longitudes and also has low proper motion, would again indicate Pi Vir, without even having considered criterion 1 or 3 at all.
 |
Choosing Pi Vir also places the galactic center within 1° of a sector boundary, adding compatibility with galactic coordinates. Thus, Pi Vir is the best origin of sidereal longitude.
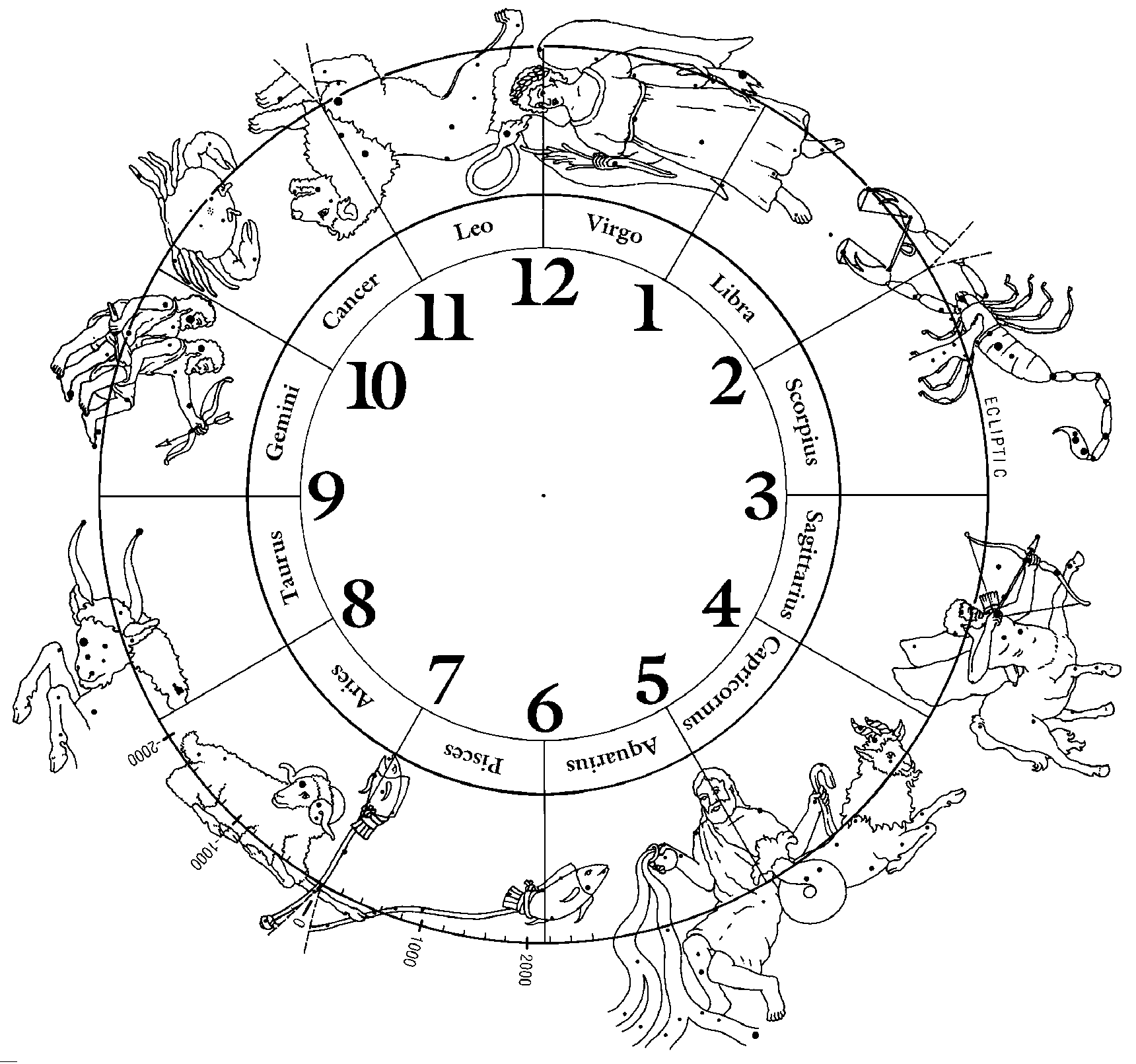
The resultant sectors of sidereal longitude are shown in Fig. 4. Note that most of the constellations fit entirely into their sectors. This illustration is the result of considerable effort to reconstruct the figures precisely according to the descriptions of Ptolemy (Taliaferro, 1952), enhanced with even older representations, such as from the temple at Dendera, Egypt (Description de l'Egypt, 1809-1828). They are the source of the figure of the scales as well as the "cloak" of Sagittarius having originally been two wings. It is a stereographic projection, which preserves shapes well, modified by cutting the sectors apart below the ecliptic (indicated by the dashed lines) in order better to preserve sizes. Note that because the constellations fit well into the sectors that only minor parts of a few constellations are cut. A scale is provided on the ecliptic between Aries and Aquarius to show the position of the uniform vernal equinox from -2000 to +2600. The longitude of the mean equinox (V) in the new sidereal coordinates is given by V = 183.83792° - 1.39629°T - 3.0903 x 10-4T2, where T is in tropical centuries from 1900.0 (derived from Allen, 1976). Similar scales could be added to the other three quadrants for the other equinox and solstices.
Because the cord of Pisces marks the zero-point, the scale can be applied to other maps as well. For example, in the woodcut in Fig. 1, the vernal equinox at the heart of the ram is about 9° (nine black/white dashes) before the stars in cord, corresponding to a date of -9° x 72 yr/° = about the year -648! (This result can be verified from the scale in Fig. 3). It is clearly a mistake in the woodcut, which purports to show the constellations for A.D. 1532, (complete with the latest garb). The intent must have been to show the equinox at the next sector boundary in Pisces, corresponding to +21° x 72 yr/° = about the year 1512. Thus sidereal coordinates facilitate both easy visualization of and calculation of the location of the equinox.
It is suggested that one reason the constellation figures have been so popular throughout history is that they can be used as a precise map for finding celestial objects without numerical coordinates. Hence, it is proposed that standardized figures, based on the classical Greek descriptions, be restored to some star atlases. It is furthermore proposed that a sidereal coordinate system could be useful to astronomers and historians alike. It could use the invariant ecliptic plane as the reference circle and fix the origin of longitude to the star Pi Vir. This star has low proper motion (a "fixed" star) and has the advantages of producing visible coordinates that also best fit the twelve zodiac constellations into 30° sectors. The choice also lends itself to a very simple definition of a uniformly precessing vernal equinox: Vu = 210° - T/(72 yrs/°).
Allen, C.W. 1976, Astrophysical Quantities (London: Athlone Press), p. 20.
Allen, R.H. 1963, Star Names, Their Lore and Meaning, (New York: Dover), p. 465.
Description de l'Egypt 1809-1828, (Paris: Commission des sciences et arts d'Egypt).
Grasshoff, G., 1990. The History of Ptolemy's Star Catalogue. Springer-Verlag, New York.
Hirshfeld, A., Sinnott, R. 1982, Sky Catalog 2000.0 (Cambridge: Sky Publishing).
Lovi G., Tirion, W. 1989, Men, Monsters and the Modern Universe (Richmond, Va.: Willmann Bell), p. 43.
Martin, E.L., 1976. "The Celestial Pageantry Dating Christ's Birth." Christianity Today, Dec., p. 280.
Mair, G.R. 1960, Phaenomena, in Callimachus, Lycophron, Aratus (Cambridge: Harvard U. Press), pp. 195-299.
Mills, A. 1989, "More Than Just Time," Sky and Telescope, Vol 79 (April 1990), p. 359.
Pratt, J.P., 1990. "Yet Another Eclipse for Herod". The Planetarian, 19, No. 4, pp 8-14.
Ridpath, I. 1989, Norton's 2000.0 (New York: Wiley & Sons).
Schroeder, W. 1965, Practical Astronomy (Totowa, N.J.: Littlefield), pp. 80-88.
Sinnott, R., 1968. "Thoughts on the Star of Bethlehem". Sky and Telescope, 36, 384.
Snyder, G. 1984, Maps of the Heavens (New York: Abbeville Press), p. 62.
Taliaferro, R. C. 1952, The Almagest, by Claudius Ptolemy, in Great Books of the Western World (ed. M.J. Adler; Chicago: Encyclopedia Britannica), vol. 16, pp. 234-258.
Toomer, G.J., 1984. Ptolemy's Almagest. Duckworth & Co., London.
van der Waerden, B.L. 1974, Science Awakening, (Oxford, 1974), vol. 2, p. 97.