Bible Codes: A New Approach

by John P. Pratt

Reprinted from Meridian Magazine (25 Jan 2006).
©2006 by John P. Pratt. All rights Reserved.

Index, Home

Contents
1. Dizzy Bear
2. History of Bible Codes
2.1 Code Breakers
2.2 Criticisms
2.3 State of the Art
2.4 Weaknesses
3. New Approach
4. Torah Tutorial
4.1 CELS encoding
4.2 Two Witnesses
4.3 Spanning Codes
4.4 Reverse Codes
4.5 Linked Codes
4.6 First Occurrence
5. Back to Eden
5.1 Wheat from Chaff
5.2 All in "Garden in Eden"
5.3 A Mandala
5.4 Contextual Crosses
5.5 Overall Probability
5.6 Adam Centered in Eden
6. Conclusion
Notes

Tarnished "Bible codes" may yet shine under new light.

Nearly a decade ago, controversial "Bible codes" were widely publicized, which supposedly proved the existence of God by the discovery of secret coded messages in the Hebrew text of the Torah (the five books of Moses).[1] Then the hype fizzled when critics unveiled similar messages in English in secular texts such as Moby Dick, which were obviously due to random chance.[2] The final nail in the coffin seemed to be a scientific refutation in 1999 to the professional paper which had given it credence in the first place.[3] Now, like the phoenix rising from its own ashes, the Bible code phenomenon may be returning as a renewed wave of interest is growing, based on new discoveries which claim to overcome the objections. After reading one of the latest books attempting to revive the subject, Bible Code Bombshell by Edwin Sherman,[4] I felt that some of his claims were true but that others were not. To me, what is needed is a new approach which can separate the wheat from the chaff.

After a brief historical summary, this article enumerates my specific objections to the way the current research is being conducted, proposes what seems to be a better approach, and then tries it out on a few verses of Genesis. Preliminary results seem encouraging enough to share, even though the new theory is currently only in the prototype stage.

Is it possible to determine with virtual certainty whether or not an author intentionally used the proposed Bible code method to encrypt secret messages into any text? That may be an important question for those who have studied Bible codes because debunking methods have left disillusioned believers with the impression that any message whatever can be found in any sufficiently large text, so it seems to follow that one could never know with confidence whether a given message was indeed really encoded intentionally by the author.

Before discussing the actual Bible codes, let us attempt to answer that question by considering an example in English I wrote to illustrate the proposed encoding method: the allegory of "Dizzy Bear".

1. Dizzy Bear

Brent received a birthday card from his father with the following weird verse:

"Dizzy Bear" Brent: neater, no, nuttiest
Brent; rambling,
Big and ageless.

Brent wondered what it meant. He knew he might look like a big, rambling bear, and that he had been called "nutty" at times, but never "Dizzy Bear" nor "ageless."

His father liked puzzles, and Brent had received cards from him before with acrostics hidden in the verse. Sure enough, his initials D.B.B. were the first three letters of each line and also of each of the first three words of the first line. That explained at least the first letters of the nickname "Dizzy Bear", but he suspected there must be more. The words "neater, no" stuck out like a sore thumb.

He took it to one friend for help, but the reply was, "I do not believe in poetry puzzles, so it would be pointless for me to look for signs of intelligent design in poetry. That just isn't scientific, because even if I found something, it could never be proven that it was not the product of random chance."

So Brent gave the card to his mathematician friend JoAnn. She agreed to be open-minded enough to look for hidden codes. She started her investigation with the word "neater" which just didn't seem to fit, and soon discovered that starting with the "B" in "Bear" and counting every third letter, it spelled out "Brent." She calculated that there is only about a 1/5,000 chance that a 5-letter word that described the subject would appear encoded by chance with equal letter spacing in such a short text, and such that it formed a perfect cross (See Figure 1).[5] So she felt she had discovered an encoded word which the author must have had in mind.

Figure 1. Lines spaced by 3 letters.
She felt there must be more. It didn't explain the other weird words, such as "no" and "ageless." So, based on her discovery, she used the scientific method by hypothesizing that other words describing Brent could be found hidden in the text using the decoding method of counting a fixed number of letters, skipping spaces and punctuation.

She found another encoding of "Brent" crossing through his name in the text, this time counting every fifth letter, and again beginning on the "B" in "Bear". Her hypothesis had correctly predicted a future discovery, which is the whole point of the scientific method. She estimated that there is only a 1/1,000,000 chance that an average topic word of 5 or more letters would be found crossing itself twice in so short a text.[6]

When she tried extending the second discovery, it spelled out "DBrentBriggs," even including the capital letters. She knew his surname was Briggs, so this put it so far beyond chance that she didn't bother calculating the odds. She now knew that the code was real.

But what about the "D" in "DBrent Briggs"? It is capitalized, just like the other two names, and those letters exactly span the entire text, as if by design. Was "Brent" really his middle name? Suddenly the double acrostic jumped out at her, and there was no doubt in her mind that his initials were indeed D.B.B.

If his surname "Briggs" was encoded, then perhaps his first name was also. She started counting letters from the only capital "D", following the example that "Briggs" was capitalized. Sure enough, in no time she discovered the name "Dan" by counting every seventh letter. What are the chances of another name just appearing like that, starting on the capital letter indicated by the acrostic? She felt it just had to be right.

JoAnn reported back to Brent that she had cracked the code. She proudly announced that she had discovered that his full name was "Dan Brent Briggs." To her dismay, Brent told her she was wrong! She begged for another chance, which of course he granted.

When she reconsidered her reasoning, everything looked perfect up to actually discovering his first name. There was no question that the names Brent and Briggs had been coded according to her hypothesis. And "D" just had to be his first initial because of the acrostic. The mistake must have been to accept "Dan" as the first name found. She realized that it was not improbable to find a 3-letter name there just by chance, even in a short verse. All she would have to do is find the next vowel and then count that same number of letters and land on a likely consonant. Maybe his name was "Don". Wishing that she had done so before embarassing herself, she now calculated that there is nearly a perfect chance of finding at least one 3-letter name starting on that very "D."[7] She had allowed her enthusiasm to cause her to announce results prematurely.

To make it easier to find names, she wrote out the verse in lines spaced by five, being the spacing between the letters of the second encoded "Brent" she found. Mathematics told her that encoded names with any spacing would show up in straight lines in that diagram if the lines were extended at the edges to repeat letters if necessary. She was then shocked to find "Den" (short for Dennis) spaced at both 6 and 11, "Dog" (a nickname?) spaced at 21, and "Dil" (short for Dilbert) spaced at 26.[8] And there could be even other longer names. How could she know which was right? Or maybe those are all there by chance and his first name is Dumpelstilskin, too hard to encode, hence only abbreviated. How could she possibly tell which name, if any, was correct? Maybe there was no new revelation to discover.

She now realized what a huge advantage it had been to already know that his last name was Briggs. She persevered and finally discovered the name "Dennis" by extending out the name "Den" she had found spaced every eleventh letter. She squealed with delight when she found it also ended on the very last letter of the verse, as did "DBrentBriggs" (see Figure 2). She calculated that the chance of finding a common six-letter name, which also followed the established pattern of spanning the verse, was only about 1/18,000.[9] Now there was no doubt that "Dennis" was the name purposely hidden in the codes by its author, and she was right.

Afterward, Brent went to his father, the creator of that one verse (or uni-verse), and thanked him for having taken the time to write it and code it so cleverly. His father was grateful that his son had believed in him enough to study his words carefully. Brent then asked if the inclusion of the second name "Den" was there by chance or by design. His father replied that he didn't plan that name at all, but it was there only by chance, even though it also followed his coding rule of intersecting the name "Brent" in the text.

Figure 2. Lines spaced by 5 letters.
This allegory illustrates the "Bible code" method of encoding as well as one trap which some Bible code researchers fell into, that of finding many codes that are probably irrelevant. But it also illustrates the importance of the context. It was not just any five-letter word that was found crossing itself twice, it was the word which described the topic being discussed. It was not just any name, or any message, nor even a nickname, which was found. It was the real name of the person to whom the verse was written.

The probability of finding an example produced by chance of the full name, consisting of at least 12 letters (which could include up to 2 initials) of a person mentioned in a text by their own first, middle or last name (consisting of 5 or more letters), encoded within 100 consecutive letters which include that name, such that both the full name and one of their three names (of 6 or more letters) exactly spanned each other, and also with the contextual name again encoded in a perfect cross, is about one in 14,000,000,000,000,000,000,000.[10]

To grasp the magnitude of that number, it means that if there were a biography of every person who had ever lived on earth since Adam, that mentioned one of their names a thousand times, and an equal number of novels and news stories had been written that did likewise about real or imaginary people, and then all of that literature were searched to find an example meeting those criteria, there would only be a one in a hundred million chance of finding even one success![11] And that is not even requiring that all of the encodings have the first letters of each name capitalized, nor requiring the double acrostic, as in the "Dizzy Bear" example! Thus, if the coding is structured well-enough, then it becomes clear that it didn't occur by chance.

2. History of Bible Codes

The history of the discovery of Bible codes is available in detail in several books,[12] and in at least one mostly unbiased summary on the internet.[13] It has long been a Jewish tradition that codes are hidden in the Torah. The Torah (which means "law" in Hebrew) consists of the five books of Moses, being the first five in the Old Testament: Genesis, Exodus, Leviticus, Numbers, and Deuteronomy. The idea of the existence of such codes fits well with another tradition that the Torah was revealed letter-by-letter to Moses and that there were originally no spaces between the words, nor vowel markings. In Hebrew, the letters are mostly consonants, read from right to left, with the vowels written as tiny marking below the letters. It is understood that once someone knows the language, it is easy to know what the written words mean from the context. The markings are mostly to indicate the pronunciation to beginners. That curious idea of no spaces fits perfectly with the entire concept of Bible codes, in which all of the spaces and vowel markings are not used. The other books of the Bible were not necessarily revealed in that way, so all of the initial research into Bible codes was done in the Torah.

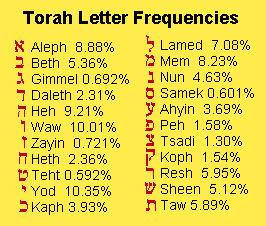
One of the first examples found was the following. Starting with the first Hebrew "t" (taw) in Genesis and counting every 50th letter, it spells out "torah."[14] That by itself could be due to pure chance and hence meaningless, but the same effect is also observed in Exodus. That is, beginning on the first taw in Exodus, and counting every 50th letter, again yields "torah." The probability of that occurring by chance in a randomly selected chapter of the Torah is only about 1 in 1800, so the possibility that such codes are real seemed to merit further investigation.[15]

This type of code, in which one finds a sequence of letters by skipping the same number of letters in succession, is called an "equidistant letter sequence" (ELS). The number of letters counted to the next letter is called the ELS spacing. The "Dizzy Bear" example used ELS codes of spacing 3 ("Brent"), 5 ("DBrentBriggs") and 11 ("Dennis").

Little progress was made from this point before computers could be used to easily do the counting for us. Excellent, inexpensive programs are now available to do this laborious job.[16] And when they were used, then it became almost too simple to unleash their power to find codes everywhere. For example, "torah" is found encoded 34 times at various ELS spacings in the first chapter of Genesis, which is about the number expected to be found just from random chance.[17] So how can we know if any of those codes were intentionally put their by the author?

2.1 The Code Breakers

Preliminary research found a lot of interesting results. A method for searching for pairs of words with related meanings was devised, and then it was determined whether a pair of such words were closer together than would be expected by chance. The idea is that even before the details of an encrypted message can be perfectly read, one can find evidence that there really is a hidden message by looking for pairs of related words near each other, such as "rain" and "umbrella."

When that method seemed to produce meaningful results, a paper was published by a peer-reviewed statistics journal in 1994.[18] With that credibility, a best selling book was written that brought the result to the public awareness, written by an investigative reporter who sensationalized it.[19] Without appreciating the underlying statistics well enough, but knowing what people buy, he immediately applied the techniques to predict the future. His book did much to discredit the entire field, for it was easily refuted. But there were also serious criticisms of the original scientific paper itself.

2.2 Criticisms

Initial criticisms were legion. Many rejected the claim out of hand simply because it was so outrageous. One of the more obvious serious criticisms is that copyist errors over the centuries in transmitting the text to us certainly must have destroyed the integrity of original text, even if it had contained encoded messages. One response to this criticism is that there are amazingly few differences in the several versions of surviving texts. It is claimed that the three principal versions of the Torah only differ by a total of 9 letters.[20] It is said that those errors are so few because the copyists were told that the universe would come to a crashing halt if they made any errors. Codes or not, a tremendous debt of gratitude is owed to the Jews for having preserved the text so well.

But even a few errors in the text will cause errors in the codes over any interval containing an error that either adds or deletes a letter. Another response to this criticism is that we are talking about God as the author, and he could know ahead what letters would be left out, and could have planned for that contingency. Thus, some researchers look at codes separated by thousands and even hundreds of thousands letters, and take them very seriously.

More serious criticisms of the work deal with what is sometimes called by statisticians "snooping" and "tuning." Snooping occurs when one peeks ahead at the data, and then proceeds to calculate the probability of that data being found using assumptions based on not having looked ahead. Tuning refers to changing ones definition of what constitutes a success to fit the data which has been snooped. Most often, these two cardinal sins in statistics are committed inadvertently rather than maliciously.

The demise of the scientific paper on which so much was based came mostly from tuning criticisms. It was pointed out that many of the rabbis whose names were found associated with their birthdates were called by appellations that worked. This is a classic example of tuning. When all names of the rabbis were included to allow for failures, the effect was found to disappear.

2.3 State of the Art

What are the new discoveries being claimed that are renewing interest in Bible codes? Those which appear most impressive are 1) there are numerous multi-word ELSs that make sense, 2) obvious focal codes are surrounded by numerous improbable ELSs, 3) there is an excess of ELS "crosses," where the same word is found encoded many times sharing a letter (as the "Brent" cross in Figure 1), 4) ELS codes appear many more times than expected, and 5) there are very compact subclusters on a single topic. Comparing the discoveries to the "Dizzy Bear" example, first the word "Brent" was discovered encoded, but later his entire name was discovered, which really removed all doubt that the code was real. All of these five examples are taken directly from Bible Code Bombshell.[21]

For me, the problem is that when I read the early chapters of the book dealing with the above, I was grateful that finally that work was progressing, and that I could rest easy that someone else was doing it just fine. But then as I read the rest of the book, I felt that the researchers have again had wandered off into Fantasy Land. So, rather than review the new work, I feel the need to vent my own criticisms of all of the work which has been done to date, and to offer a proposed solution.

2.4 Weaknesses

Thus, let's consider a new approach which addresses these weaknesses in the current theory.

3. New Approach

There is one element of nearly all of the more convincing codes discovered, which has never been formalized into a requirement. Different authors have commented on attempts to do so, but it just doesn't seem to fit into an objective approach very well. It is that the codes must relate to the topic being discussed in the surface text. To me, that is the grand key to most, if not all, of the Bible codes. All five of the above mentioned new findings which are most convincing have various ties to the surface text. But when this requirement is not included, then all sorts of discoveries are included as valid which to me are not.

What I propose is that a subset of ELS codes be considered. The requirement is so new and different from what has been done, perhaps they should have a different name. Let us call them Contextual Equidistant Letter Sequences (CELS). That is, the code must relate to the context in which it appears, or else it is rejected as random. When the spacing is so large that a variety of subjects are discussed in the surface text, then at least one of the words intersected must clearly relate to the encoded word.

This contextual requirement is a little slippery, and opens the door to "tuning" criticisms. What one person thinks relates, another does not. But sometimes it is crystal clear. In the "Dizzy Bear" example, the encoded words "Brent", "Briggs", and "Dennis" all intersected the word "Brent" in the text. Note that such is only possible if the encoded word contains the very same letters as the contextual word ("Dennis" contains both an "e" and an "n" as does "Brent"). This is a very stringent requirement. It is an extreme case of what the original statistical paper was using as a metric. Those researchers required that the two sought terms intersect "near" each other. My proposal is that they intersect in exactly the same letter, and moreover, that at least some letters be contained in a related surface words. While that method may seem harsh because it eliminates so many codes, it also allows other codes to be accepted because no longer is there a requirement for two words, nor long words. A single short encoded word might be meaningful if it is composed of letters found in meaningfully related words. A preliminary attempt at an objective way to determine which words are related is proposed below, but first let us consider what might be a "Bible Code Tutorial".

As mentioned above, some of the first ELS codes found were of the word "torah" right at the beginning of the Bible. If that is meaningful, why would the word "torah" be used? Because the codes only occur in the Torah? I don't think so. Let's consider another idea. Suppose "torah," which means "law," was chosen to show examples of the law which governs the Bible codes. If so, some encoded "torah" words may have been designed as a tutorial to show exactly which are true codes and which are spurious. Let's try that hypothesis.

4. Torah Tutorial

Let's look in more depth at one of the first codes discovered. First, we need a notation to indicate a specific letter. The usual notation of Gen 1:1 means Genesis (chapter) : (verse) . The notation adopted by Bible code researchers is Genesis (chapter) : (verse) : (word) : (letter) . That is possible because the verses are also indicated in the Hebrew text. If we don't read Hebrew, we might also need an interlinear Hebrew-English Bible, to see the translation of each word.

Torah Letter Frequencies
Table 1. Torah Letter Frequencies.

4.1 Lesson 1: CELS encoding

Starting with the first Hebrew "t" (taw) in Genesis, and counting every fiftieth letter, we find the following four indicated letters: Gen 1:1:1:6; 1:2:8:3; 1:4:1:3; and 1:5:2:3. The four words containing those letters are Gen. 1:1:1 "In the beginning," Gen. 1:2:8 "the deep," Gen. 1:4:1 "and saw," and "Gen. 1:5:2 "God." Those four words are not all only meaningful, they form a sentence in the correct Hebrew order: "In the beginning, God saw the deep." That is a bull's-eye for the new theory that at least some of the words in the surface text need to be key words in that context. In this case, they are not only key words, but they also form a sentence similar to the opening sentence of the Bible, "In the beginning, God created the heavens and the earth." If the ELS spacing had been 43 instead of 50, then the four words would have been "In the beginning," "on," "let be," and "between" and the new theory might have rejected this famous ELS as invalid (except for the word, "In the Beginning," which might salvage it). Note that it has already been rejected by the currently accepted theory, because it did not appear in a closely related pair of words, and also it was just one of the number expected statistically to be in that chapter.

Now that we have examined this code more carefully, three new experiments suggest themselves to extend the theory:

4.2 Lesson 2: Two Witnesses

Let's use these new hypotheses to do another experiment. The statistical paper which made the codes famous found valid codes only in Genesis. Let's test our theory by looking for "torah" at an ELS of 50 at the beginning of the first chapter of Exodus. Of course, here we are repeating an experiment that was done long ago, but it is recommended in science to repeat experiments to verify and extend results. The four words indicated in this long-known ELS for "torah" are Ex. 1:1:2 "the names of," 1:2:4 "and Judah," 1:5:5 "the loins," 1:6:7 "that (generation)." Again those words all seem related, and might form a meaningful sentence or idea. But here we must be cautious. It is not too surprising with a such small ELS spacing, which selects all the words from a similar context, that the words seem related. This contextual rule is more useful to eliminate long ELS spacings, but can also eliminate short ELSs which hit no key words.

Thus we have a second witness that the codes are real, and support two of the hypotheses proposed from Lesson 1. That is, the code was found with spacing of 50, it was found in meaningful surface text words, but it doesn't clearly span any concept.

Now let's do a spanning experiment, to see if that concept leads anywhere.

4.3 Lesson 3: Spanning Codes


If the first "torah" code was indeed intended to suggest to us that a valid code might be used to span a text, then one possible experiment is to look for another spanning code. The concept of spanning occurred to me as I wrote my "Dizzy Bear" example. It was written before the following experiment was done. I made a point in that verse to pick an exact number of letters that would work to encode both "Dennis" and "DBrentBriggs" beginning with the very first and very last letter of the text, to indicate to the decoding person that I was purposely taking advantage of the fact that both names began and ended with the same letters. To me that would be a clear indication of order, because it required the exact number of letters to have been chosen by intelligent design before even a single word had been written.

So in preparing for this article it occurred to me that the Lord might have used the same idea. The first experiment I thought of was so successful that I feel only to include that one example. Chapter 1 of Genesis spans the activities of the entire six periods of creation. What if one "torah" code spanned that entire chapter? I looked at the last word of the chapter and it begins with heh, the same letter that "torah" ends with. The taw in the first "torah" is the last letter of the first word of the chapter. That in itself shows an ordering which is common with the Lord, that the last is first and the first is last. Moreover, the first letter is found in the word "In the beginning" and the last in the word "sixth" which exactly describes what section is being spanned.

Thus, the experiment was to see if the middle two letters of "torah" are found in exactly the right positions in the text to form a spanning code with these two letters. The chance of that occurring in a randomly selected text from the Torah is only about 1/500.[23]. Most statistics studies only require a probability of 1/20 to be considered meaningful, so this seemed like a good test. Of course, if it failed, it might only mean that the Lord did not choose to encode that word in that manner.

The experiment was a success. The word "torah" is indeed found in an ELS sequence of spacing 554, the only possible spacing to join the two letters indicated. Looking at the two words containing the other two letters, they are "its" (Gen 1: 12:12) and "morning" (Gen. 1:23:4), which do not seem meaningful. If this code is real, as appears to me, then the results of this experiment indicate 1) that the ELS spacing does not always have to be 50, 2) an ELS might span an entire chapter, and 3) not all of the surface text words of a spanning ELS need be meaningful. The purpose of the code might be only to show that the encoded word applies to a particular text as a whole, rather than only a single word therein.

4.4 Lesson 4: Reverse Codes

Now let's try the experiment of looking for "torah" encoded at 50 in the first chapter of the other three books of the Torah. Checking Leviticus, we find no "torah" encoded at spacing 50 anywhere in the first chapter, much less beginning in the first verse. There is a 1/15 probability of finding it somewhere in the chapter by chance, so if one had been found starting after the first verse, it may not have been meaningful anyway. Let's continue the experiment before making any conclusions.

In Numbers, "torah" is again found encoded beginning in the first verse, but this time the word is in the reverse order, starting with the heh and spelling "torah" backwards. Reverse codes are well known in Bible code research, and are indicated by a negative skip distance, -50 in this case. It can be thought of as finding the last letter first and spelling the word backwards, or if the first letter is found first, then one counts backwards to get the next. Because the implied tutorial led us directly to examine this verse, to me it means that reverse codes are as real as the forward codes. Of course, both need a lot more evidence to have a truly compelling proof of their existence. In this case the surface text words also seem meaningful (Num. 1:1:4 "Moses," 1:1:16 "Egypt," 1:2:12 "names," and 1:3:10 "them") because the first chapters are about Moses recording their names and numbers.

A side discovery here, which was not part of the experiment, might be useful in designing future experiments. There is only a 1/16 probability of finding even one "torah" at spacing 50 in Numbers 1, but two were found. The other is a forward code ending in the very last verse. Again that indicates much more order than merely having been found at some random place in the chapter, as would be expected by chance. And again we see the first and last, with reversals. That code looks real to me.

Checking Deuteronomy 1 we find "torah" once in chapter one, ending in the next to last verse. It has meaningful surface text words (Deut. 1:42:14 "You be struck" 1:43:9 "and acted proudly," 1:44:9 "as," 1:45:4 "Jehovah"). That is very similar to the finding in Numbers of a code near the very end of the chapter, rather than at the very beginning. It cannot be counted as a success for this experiment, but it might be a clue to how the codes are used at the beginning and the end.

Thus, technically, the experiment failed for all three of the books of Leviticus, Numbers, and Deuteronomy, because I was looking only for forward ELS codes at the beginning of the first chapter. Had I been looking for reverse also, then Numbers would have been a success, but the odds would have been twice as likely to have been there by chance. In science we often learn more from the failures than the successes.

4.5 Lesson 5: Linked Codes

Now let us return to Leviticus. If indeed the Lord set all of this up as a tutorial, then surely he would not leave out Leviticus, which contains no code for "torah" at spacing 50 in the first chapter. Before writing this article, I decided that if there were no lesson for us in Leviticus, then I would cancel the article, because everything discovered so far in these experiments really could all have happened by chance. We have not yet found a "killer code" which is truly compelling.

There is a principle in Hebrew writing called "chiasmus," which is that when one finds repetition at the first and last, then look to the middle for what is the most important. We have found forward codes at the beginning of Genesis and Exodus, and also at the end of the first chapters of Numbers and Deuteronomy. If the Lord is following a chiasmus pattern, then the most important code should occur in the first chapter of Leviticus, the middle of the five chapters.

Looking there we find something very interesting, which has hitherto been overlooked as far as I know. Starting in the second verse, there is a reverse code for "torah" with spacing -60, and then beginning on its final "taw," there is a forward "torah" at spacing 40. The fact that 40 and 60 average to 50, which was what we were looking for, might be intentional. As a working hypothesis, let's suppose that the tutorial is real, and that the lesson here is that encoded words with different ELS spacings can be linked by sharing a letter.

There are two very intriguing aspects of linked codes. First, they increase the amount of order and are less probable than separate codes. To convince yourself of that, imagine that two examples of a very rare code have been found in a very long text. For example, suppose "Adam, the first man" were found at two different ELS spacings in Genesis, when one would not expect a phrase that long to occur even once. Now, out of all the places they might have occurred, suppose that they both share the same "A" as the encoded letter for "Adam." Without doing a lot of calculations, it is hopefully obvious that such would be much less likely than having two separate sequences.

The second nice feature of linked codes is that it consumes fewer letters for encoding. Why use up eight letters for two encodings of "torah" when seven will do. In fact, we have already seen this. The same taw was used in the original "torah" found with spacing 50, and in the spanning code of spacing 554.

As I thought about how far this principle of "economy of letters" could be pushed, I wondered what is the most codes per letter that is possible? This may be an important question for short words. Most Hebrew word roots contain only three letters. And yet three-letter ELS codes can happen so frequently that many Bible Code researchers reject all of them because they have no way to tell which are real or not. The name "Dan" really did appear in the "Dizzy Bear" verse, complete with the capital "D," without me having planned it. But now suppose that my friend's name had indeed been Dan? How could I have encoded the verse to make it clear that "Dan" was not there by chance?

Figure 3. "Tom" encoded 7 times.
One answer is that it could have been encoded many times, using linked codes to minimize the number of letters per encoded word. It could form a pattern which could make it perfectly clear that it had been designed. I wrote the following sentence for my friend Tom to illustrate the point:

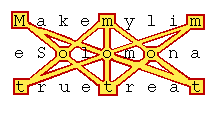"Make my lime, Solomon, a true treat."
When written as three lines of nine letters each, the name "Tom" is found encoded seven times using only nine letters (See Figure 3). I do not see how anyone would need to calculate any probabilities after seeing the pattern to convince themselves that these seven occurrences of "Tom" in only 27 letters of text could not have been due to chance. I could have included one more "Tom" in by using "demo" instead of "lime," but chose not to because that would have decreased the ratio of codes to letters and also would have marred the pattern. After I created this illustration I recognized the pattern as one form of the "mandala" which is believed to have been used in Egyptian figures. Hence, I'll refer to this pattern as the mandala.

Thus, this important lesson from Leviticus may be a key to recognize encodings of three-letter Hebrew words.

4.6 Lesson 6: First Occurrence

Another experiment occurred to me. If the surface text is so important, then one might expect that the first time a word appeared there, it might be accompanied by explanatory CELS codes. To test that theory, I looked at the first occurrence of "torah" in the Torah, which occurs at Ex. 12:49:1. It turns out that there are four ELS codes for "torah" in that chapter that intersect that very word. In itself that is not amazing; one or two occurrences are expected just from random chance. Checking the surface text, we find that two of them indeed appear to be random, whereas two are CELS codes which tie to the context. Moreover, those two are both examples of the very codes we have already discovered. One has a spacing of 50.[24] If we had been looking for that, the chances would only have been about 1/280 of finding it.[25] Moreover, the other code with spacing of -903 exactly spans back to first "heh" in "Jehovah," being the second word of the chapter, at Ex. 12:1:2:2. Again, had we been explicitly looking for such a code, the chances would again be about 1/500 of finding it.[26] To me this is a confirmation of the proposed concept of spanning, because it spans an entire discussion of the law of the Passover and its first celebration (Ex. 12:1-49)[27] as well as the possibility of "first occurrence" codes.

5. Back to Eden

Let's now try out the new theory on an early discovery from Bible code research which has been mostly ignored, if not entirely rejected, even by most researchers. Early work found that the three-letter Hebrew word "Eden" appears encoded far too many times in a short section of Gen. 2 to have been likely to be by chance.[28] This encouraged researchers at the time, but the discovery was just one among many, and has been largely passed over as more sophisticated techniques were developed, focusing on more improbable longer words. In fact, most researchers do not take three-letter discoveries seriously because they appear so often.

This seemed like a good example on which to test my new theory, that if those excess codes were truly put there on purpose by the author, then 1) they should be CELS codes which explain more about either specific key words they intersect, or sections of text they span, as in the "Dizzy Bear" example, or 2) they could show patterns of maximizing the number of encodings while minimizing the number of letters, as in the mandala pattern of "Lime Treat". My current theory discards all codes which do not meet either of those criteria. Moreover, because this passage contains the first reference to Eden, it seemed qualified to test the hypothesis that the first time a major concept is introduced, there might be special codes around it to explain it better.

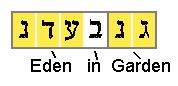
I checked out every occurrence of "Eden" as an ELS of any length greater than one and looked up what word each letter occurred in, using an interlinear Hebrew English Bible. After sufficient data snooping (which can be compensated for when calculating probabilities), I decided to focus on Gen. 2:5-10, containing 329 Hebrew letters. In a passage of that length chosen randomly from the Torah, one would expect to find the three-letter Hebrew word "Eden" about 5 times just by chance. Note how prolific these codes are. If one did not calculate probabilities, it might appear amazing to find any word encoded five times in such a short passage. But in this case, "Eden" appears in ELS codes 15 times. The probability is less than one in 8,300 for that to occur by chance in a random passage,[29] so this looks like a fine place to see if context can help us determine which codes might be real and which are not.

5.1 Result 1: CELS separates Wheat from Chaff

An attempt was made to verify the CELS hypothesis by identifying about one quarter of the total number of words in the text as "key" words relating to the garden of Eden. That was a larger fraction than the goal of at most one tenth I had arbitrarily set, but they all seemed important. In a longer text, the key words would hopefully comprise a smaller fraction. Those twelve words were also put in a proposed order of importance, for the purpose of attempting to calculate the odds of intersecting them. I realize there is subjective bias in any such proposal, but one needs to begin somewhere. Counting all the times they were used, these words contained almost exactly one quarter of all of the letters in the text.[30]

By checking the surface text words, nine ELS codes were found that intersected key words in the surface text in a meaningful way, while six did not.[31] By the new theory, those nine would qualify as CELS codes, and the other six are discarded as having been caused by chance. Thus, to me this was encouraging, because it so closely matched what probability predicts, namely, that there would be about five ELS codes found by chance alone. But this result is not compelling because there is a better than an even chance that any one ELS will intersect some key word.[32] This is tricky business; nevertheless, it is hopefully a step toward separating out real codes, if there are any, from wishful thinking. It turns out all nine of those CELS hits are impressive for other reasons, as we shall now see.

Figure 4. "Garden in Eden."

5.2 Result 2: All CELS codes intersect "Garden in Eden"

The second result is much more important. All nine of the proposed CELS codes intersect the same instance of the two most important key words: "Garden" and "Eden" in Gen. 2:8. The chances of that happening in a randomly selected text is only about 1/118,000.[33] In other words, all we knew at the start of this experiment was that there were 15 encodings of "Eden" scattered through those six verses of text. Now we discover that all nine of the CELS codes exactly intersect the first time the words "Garden" and "Eden" appear in Genesis, which is a much less likely event. Moreover, seven of those nine CELS codes intersect what to me is the one topic summary word of the entire passage: "Eden."

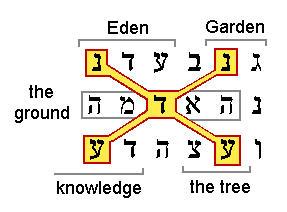
Now we shall see that those CELS codes not only all intersect the two most important words, they also form meaningful patterns. Those nine words fall into three groups. One of the nine intersected only key words. That one had an ELS spacing of 83, and comprised the letters Gen 2:5:8:1 in "herb," 2:6:9:3 "ground," and 2:8:5:4 "Eden." Four of the nine formed a nearly complete mandala figure as in the "Lime Treat" example, and the other four formed two crosses in meaningful contextual ways. Let us now consider the strength of those patterns in more detail.

5.3 Result 3: A Mandala

Perhaps the most important result and the biggest clue that the codes are "real" is the fact that all but one of the nine CELS codes found are contained in patterns that reduce the number of letters required to create the 9 codes through the phrase "Garden in Eden." In fact, four of the codes form a pattern which is strikingly close to the mandala pattern in "Lime Treat".

Figure 4 shows the words "Garden in Eden" as they appear in Gen. 2:8. Remember that Hebrew reads from right to left. The word "Garden" has two letters, "in" has one, and "Eden" has three. This figure was included to help you recognize the word "Eden" to better appreciate these results.

Figure 5. An Eden Mandala.
Figure 5 is a matrix of letters much like those in the above "Dizzy Bear" and "Lime Treat" examples. These Hebrew letters are taken from the verses being studied, and are spaced at 52 letters between lines. The word "Eden" in the middle is the focus word from Gen. 2:8:5. Notice the word "Eden" again at the bottom, being the only other time this word appears in the passage (Gen. 2:10:3). Now it just so happens that three other letters are placed in exactly the positions needed to produce four of the CELS encodings. Note that the figure produced is almost identical to the "Lime Treat" mandala, except that it is missing one corner and turned onto its side. Of course, the word "Eden" is actually spelled out six times in this figure, two being in the surface text, but I am only counting the other four. That is not generosity on my part; these verses were chosen because they were about the topic of Eden, and hence it is expected that the topic word will appear a few times.

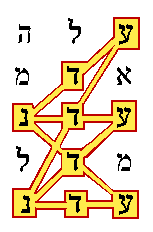Do any of the three letters which complete this figure occur in key words? The answer is that only one does, but probably two should have. The word on the top row is in "went up" where it states that "there went up a mist from the earth" (Gen. 2:6:2:2). To me that is not a key word. The word in the next row is "the ground" in Gen. 2:7:8:3, which was chosen as a key word. The word in the row between the two "Edens" is "pleasant" (Gen. 2:9:8:4) which perhaps should have been included in my list of key words. It is practically a synonym for the whole idea of the Garden of Eden. This is where the temptation arises to "tune" the definition of a "success" by going back and changing the list of key words. But "Eden" also sounds like a good place to avoid temptation, so I will resist the urge.

The chances of this much of the mandala pattern occurring around the two words "Eden" in a text from the Torah, and including at least one contextual keyword are less than 1/39,000.[34] Note that this pattern approach is starting afresh to calculate probabilities. There is only a 1/39,000 chance of finding such a nearly complete mandala, without even considering the other 11 "Eden" encodings found in these six verses.

Figure 6. A Contextual Cross.

5.4 Result 4: Contextual Crosses

The last four of the nine CELS codes which intersect those same first occurrences of "Garden" and "Eden" form part of what could be called a "contextual cross" structure. A contextual cross is an "X" shaped pattern which connects one pair of surface words (in this case "Garden" and "Eden") to another pair of meaningful surface words. Let's look at each of these crosses.

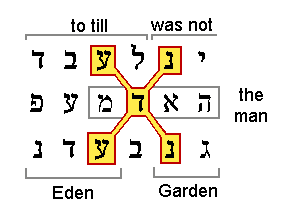When the spacing between rows is changed to 59 letters, we see in Figure 6 of the type of cross meant. The two words "Garden" and "Eden" appear to be connected to the words "was not" and "to till" in the phrase "there was not a man to till the ground" (Gen. 2:5). What makes it meaningful is that the letter at the center of the cross appears in the word "the man." Even though none of those three words was on my key word list, it still forms a phrase: all the contextual words put together say "was not a man to till the Garden in Eden" which is nearly the same as the phrase "there was not a man to till the ground." This is much like what we saw in the very first "torah" example, where the contextual words formed another sentence much like the surface sentence.

The chance of finding such a connecting cross using the word "Eden" to connect the words "Garden" and "Eden" to any two others is 1/88.[35] For now, we will not include any factor for the five words all forming a sentence because the other three words were not on my key word list. Perhaps future studies can take this sentence-forming feature into account.

Figure 7. Linking Eden to the Tree of Knowledge.
Finally, looking at Figure 7, spaced at 43 letters per line, we see a much better example of a contextual cross. This time all of the contextual words were on my key word list. The cross connects the words "Garden" and "Eden" to the words "tree" and "knowledge" in the phrase "the tree of knowledge of good and evil" (Gen. 2:9:16-17). The connecting word is "ground" (Gen. 2:9:5:3), which indeed connects a garden to a tree. Thus, the "Garden in Eden" is connected to the "tree of knowledge," which is what the whole story is about. The probability of such a cross occurring which is composed entirely of key words occurring by chance is about 1/8,200.[36] Why is that so much smaller than the probability for the other contextual cross? Because it hit the bull's-eye of intersecting the third and fifth most important key words.

5.5 Overall Probability

So what is the overall probability of finding those three structures? That is difficult to calculate because one should first determine the entire group of exactly which structures constitute a "success." The chance of just these three structures occurring together in the same two words of "Garden" and "Eden" is the chance of the near-mandala (1/39,000) times the chance of the first cross (1/88) times the chance of the second (1/8,200), which equals 1/28,000,000,000, or one in 28 billion. Let's reduce that by a factor of 1,000 as an estimate to allow for all of the other possible structures I have failed to consider. Even so, to me a chance of 1/28,000,000 is compelling evidence that these "Eden" codes were indeed truly encoded by the Author.

Now we can finally compensate for the "snooping" done earlier. We started out with a set of six verses which for which we knew there was only a 1/8,300 chance of containing so many encodings of Eden, if there by chance. What is the chance of finding something with a 1/28,000,000 probability given that we started knowing it had purposely been selected because of having only a 1/8,300 of existing at all? The answer is that one divides the two probabilities, to get about 1/3,000.[37] So starting from where we did, there was only a one in three thousand chance of getting these results. That is far less than the usual 1/20 confidence level required for most statistical studies.

5.6 Adam Centered in Eden

Figure 8. "Adam" is centered in "Eden" in Figs 5-7.
A bonus discovery, definitely not part of my experiments, nor my probability calculations, was discovered as I was creating the illustrations for Figures 5-7. I thought I had made a mistake because the same letters kept showing up. Look at the three letters on row two of Figure 5, and at the center of the crosses in Figures 6 and 7. All of them match the three in the name "Adam" (Figure 8). The same root word, with vowel and ending modifications means "Adam," "ground" and "man." In fact, "Adam" is also centered in the first CELS code mentioned above, spaced at 83. That means that six of the nine CELS codes have "Adam" centered in "Eden." That adds another entire dimension to CELS encoding, because the same letters can have multiple meanings. Perhaps future lists of key words, which I made in English, should have the Hebrew roots taken into account. Finding six witnesses of Adam centered in Eden leaves absolutely no doubt in my mind that these codes are real, and hold the promise of great new truths and wisdom.

6. Conclusion

Equidistant letter sequences (ELS), popularly known as "Bible codes," have been abandoned by most as an unfounded fad, but new discoveries have suggested that some codes may be real after all. This article addresses problems even with the new discoveries and suggests a new approach to the entire field, which entails requiring that all valid codes be related to the context in which they appear. An attempt was made to interpret what might have been a "tutorial" included in the five books of Moses, from which six principles were deduced. They eliminate most of the "discoveries" which have been published to date, which indeed appear to this author to have been caused by chance.

The ELS codes allowed by this new theory are called "contextual" ELS codes (CELS) because only codes related to the surface text can be considered as having any chance of being real. This work is only in the prototype stage, and no scientific metrics have yet been devised. Indeed, an objective approach appears elusive because the whole definition of what is "related" seems subjective. Nevertheless, as a first application, with an eye toward developing a rigorous scientific method later, a study was made of only one occurrence of two words in the Hebrew Genesis: "Garden" and "Eden". The precise words in which all of the letters of the fifteen ELS sequences for "Eden" in Gen. 2:5-10 were examined, and nine were found to qualify as CELS codes, all of which intersected those two words. Then patterns they formed were examined which decreased the number of letters required for so many codes. That is precisely a technique that would be expected to be found in work truly encoded by the author as it would form less probable combinations, as well as leave more locations available to include other encoded words. A preliminary estimate of the significance level of this discovery is 1/3,000, far beyond the usual 1/20 required.

It must be emphasized that the results being reported here are entirely preliminary. Only one occurrence of two key words was studied using the new technique, and even then only intersections of the topic word with those two were considered. Statistics call for large samplings, and so there is much work left to be done. The only reason that it appeared worth publishing with such a small sample was that it proved so rich as to require several illustrations to show the many dimensions of just those two words. The other reason is that I plan to go back to calendar work, and hope that others will continue and perfect this new approach, if it continues to appear fruitful.

The conclusion at this early point in new research is that it appears that at least some CELS codes are real, and the contextual analysis may prove to be the key to separating true from false ELS findings. Indeed, it now appears that time might show that the Bible code phenomenon could unfold much as did the miracles of Moses to Pharaoh: the skeptical magicians were able to duplicate the first few, but then God's miracles kept multiplying until they were compelling. To me, the hand of God is being manifest in just two words of his great revelation to Moses. It is no wonder that we are commanded to live by every word which proceeds from the mouth of God (Deut. 8:3).

Notes

  1. Drosnin, Michael, The Bible Code (New York: Simon & Schuster, 1997).
  2. McKay, Brendan, "Assassinations Foretold in Moby Dick!" cs.anu.edu.au/~bdm/dilugim/moby.html.
  3. The original paper was Witztum, D., Rips, E., and Rosenberg, Y., "On Equidistant Letter Sequences in the Book of Genesis," Statistical Science, 9 (1994) , no. 3, 429-438, refuted by McKay, B., Bar-Natan, D., Bar-Hillel, M., and Kalai, G., "Solving the Bible Code Puzzle," Statistical Science, 13 (1999) 150-173.
  4. Sherman, R. Edwin, Bible Code Bombshell (Green Forest, AR: New Leaf Press, 2005).
  5. JoAnn noticed that it wasn't just a random word which formed the cross, but the very word which best described the subject of the verse. For a five-letter topic word to form a cross at any given spacing between letters, all four of the five letters around the center letter must fall in exactly the right spot. She calculated that the frequency of a randomly chosen letter from English text would be 0.0655 or about 1/15. (That number is found by summing the probability of finding any one letter, times its frequency, or simply the sum of all the squares of frequencies. She got them from the first table in "Relative Frequencies of Letters in General English Plain Text". That means if you pick a letter at random from English text, it probably has a frequency of .0655 or 1/15 rather than the 1/26 you might expect. The more frequent letters like "e" increase the average.) Thus, the probability of getting the other four letters of the word exactly right is 0.06554 or 1/54,000. There are 11 possible letter spacings (3 to 13) to fit in 56 letters if the topic word were centered, which makes the probability about 11 times higher, or about 1/5,000.
  6. When JoAnn found the second cross, it was not centered as was the first, hence, maybe it was just chance that the first one was. So she relaxed the requirment for a similiar event to be found in random text to be only that the topic word intersect itself, rather than having to be centered. So the intersection could have been through any of the five letters, and hence the probability of even the first find was about five times greater, or 1/1,000. The chance of that happening twice is roughly 1/1,000 x 1/1,000, or 1/,000,000. An important technical point that seems to have eluded some other researchers, is that latter calculation is only true in the case of independent events, such as rolling dice. But these events are dependent, meaning that once a first cross is found, there is always less chance of finding a second one for two reasons. First, one of the choices is used up, and secondly, that first one also removes several more choices because of collisions. Only if the probabilities are small is the discrepancy negligible. I calculate as if the events were independent, and then compensate by saying the real probability is less than the calculation.
  7. The chance of getting the last two letters to spell a certain name at a given spacing is (0.0655)2 or 1/233. She found nine possible names in her name book: Dag, Dan, Del, Den, Dex, Dom, Don, Dow, and Dud, raising the odds to about 9/233. Any of those names could be found at any one of 26 spacings (2 to 27), which increased the expected number of finds to 26 x (9/233) = 234/233 or 1.00. Multiplying in that manner only gives probabilities when they are small. As the number approaches or even exceeds one, the technical term is "expected value." If we had allowed the name to start in other places, then the expected number of finds would far exceed one. In this case, there were actually three found, "Den" twice and "Dan", which will happen about one time in six on the average.
  8. Note that she found two names (Dil and Dog) which were not on her list of possible names. In probability experiments, it is always tempting to relax the definition of what you were looking for to include what was actually found. But on the other hand, maybe his name really is Dilbert.
  9. The first and last letters were already determined by "DBrentBriggs," and the only possible spacing to span the verse was eleven, so the name had to have exactly six letters, starting with a "D" and ending in "s." In her name book, she found only the names Dallas, Darius, and Dennis as possibilities. At this point she could have looked up the actual frequencies of each of those letters, but she only wanted an estimate. The chance of getting the middle four letters correct is 0.06554 time 3 choices equals a 1/18,000 probability. Note how the imposed structure made all the difference: there was only one spacing possible instead of 26 as with the 3-letter name, and only three possible names rather than one of 10,000 male first names.
  10. The structure greatly reduces the number of possible ELS spacings that are possible. To have a name of 6 or more letters span the same distance as the full name of 12 or more, avoiding collisions, allows only 11 possible pairs of ELS spacings, of which only one will work for 6- and 12-letter names (namely the one used in this example). For any one configuration, the chance of getting each letter in the right slot is (.0655)22, being the requirement for 12 + 6 + 4 (in the cross) = 22 letters. Note that unlike JoAnn, I am counting probabilities of the first and last letter twice, to include the chance that the short and full names both begin and end on the same letters. The number of possible configurations was taken to be 3 possible names of six or more letters (first, middle, last) x 4 possible ways to include up to two initials (none, first, middle, both) x number of places the contextual name could be found in the spanned area (52 in the case of the example of 56-letter span), x the number of ELS's for the cross (11 in the example, being 3-13). For completeness, I also included the probabilities of all longer names calculated for every one of the 11 possible pairs of possible lengths, which increased the probability by a factor of 1.18. Multiplying all of those factors yields 7.3 x 10-23, or 1 in 1.4 x 1022.
  11. To estimate in round numbers, assume there have been 70 billion people who have lived, leading to 1.4 x 1014 references to names to check. Multiplying that times the probability of each being a success of 1/(1.4 x 1022) yields 10-8, or 1 in 100 million.
  12. One of the best summaries is Satinover, Jeffrey, Cracking the Bible Code (New York: Morrow, 1997).
  13. It was tough to find a fair summary, most accounts are either violently against them or religiously in favor. I recommend the Wikipedia article, "Bible Code."
  14. Rabbi Michael Ber Weissmandl, is usually given credit for this discovery in the 1930s (Bombshell, p. 28). It is said he wrote out the entire Torah on white cards in 10x10 arrays. (Cracking, p. 69)
  15. There are four letters in the word "torah" in Hebrew. The probability of finding the first letter taw in Exodus is 100%, because it is a common letter. The probability from Table 1 of the other three letters waw (frequency of 10.0% in Torah), resh (5.95%) and heh (9.21%) all occurring in the indicated place is found by multiplying those three frequencies, yielding 0.000548, or once in 1,820, if it resulted from chance.
  16. All Bible code results in this article were either found or verified using the program Bible Codes 2001, available from Ed Sherman's website at www.biblecodedigest.com.
  17. Sherman, in Bombshell (see footnote 1) includes equations on how to calculate probabilities, which are probably the same as those included in the Bible code program he sells (see. fn 15), which were used to calculate this expected value. His equations appear correct to me to calculate the number of possible ELS locations in a given text, so I used them when needed in this article. They are first, that "the total number of possible ELSs with L skips (including both forward or backward ELSs) that can fit within a text of T letters when the interval can be any number from 1 to N is N*(2T - L - N*L)" (p. 226). To find the maximum number that can fit in, substitute N with "M = integer [ (T-1)/L ]" (p. 229). He uses the confusing definition that L is one less that the length of the ELS sequence, so that for an encoded word of 4 letters, L=3. His equations for the expected number of hits and probability of any given number of hits are based on the Poisson distribution which only applies to independent events (see my fn. 6). It is an excellent approximation for long words encoded in large texts, but breaks down in the case studied in this paper of short words encoded in short texts. But, alas, I use the same equations, knowing they over-estimate the probabilities.
  18. The first paper mentioned in footnote 3.
  19. See footnote 1.
  20. Satinover, p. 51. Research in this article was done with what is called the Koren version, used in the Bible Codes 2001 program.
  21. Bombshell, pp. 57-74.
  22. Bombshell, p. 139.
  23. The probability is the chance of having the first and last letters spaced in a multiple of three (1/3), times the frequency of the second letter waw (.100), times that of the third resh (.0595).
  24. I found the first occurrence by searching for ELS=1 (forward only). Apparently this code was first found by Rabbi Weissmandl, but not as related to the first occurrence of "torah" (Cracking, p. 85).
  25. The probability is that of the ELS of 50 intersecting any one of the four letters in "torah" times 2 (for forward and backward). Let me define the "combinational probability" pc,r of "n" letters as the summation of the products of each of their separate frequencies, omitting "r" terms. Thus, pc,1("the") = p("t")p("h") + p("t")p("e") + p("h")p("e"), where each term omits one the probability of one letter. The letter omitted is the letter found in the surface word being intersected. Then the probability that "torah" intersects itself in any letter is 2pc,1("torh") = 1/283.
  26. Essentially the same calculation as in footnote 23.
  27. Arguments could also be made for the spanning ending in verses 42, 49, or 51. For spanning to be a useful concept, some objective definition would be useful.
  28. Jeffrey, Grant, The Mysterious Bible Codes (Nashville: World Publishing, 1998), alots the discovery one sentence, "In addition, the researchers found the name Eden encoded sixteen times in the same passage." (p. 85). I am grateful that Jeffrey included many shorter codes, for which he was chastised by more statistically rigorous researchers, but for which he may well eventually be vindicated.
  29. The expected number of occurrences is the product of the frequencies of the three letters from Table 1 times the number of possible ELS sequences greater than unit spacing from Sherman's equation in footnote 17: .0369 x .0536 x .0463 x 53,138 = 4.87. Poisson statistics approximates the chance of finding "n" values, given an expected value of "m" as p(m,n) = (mne-m)/n! That equation, which overestimates the probability as discussed in footnote 17, gives a probability of finding 15 encodings as 1/8,300.
  30. Twelve words were selected as "key" out of 49 total words. In proposed order of importance, they are: Eden (8), garden (8), tree (8), life (9), knowledge (4), good (7), evil (3), planted (4), watered (5), ground (20), herb (3), and shrub (3). The total number of letters found in all occurrences of each word is listed in parentheses following the word, with anciliary letters such as "and", "in," etc. counted as part of the word, as is done in Hebrew. They comprise 82 of the 329 letters, or 25% of the text. The probabilities of the results found in this article would have been even better if those letters had no been included; further research is needed to determine if they should be counted or not.
  31. The meaningful CELS codes have skips of 53, 53, 105, -51, -45, -41, 58, -60, 83. The random ELS codes had spacings of -117, -90, -71, -47, 107, 16. Note that the 16 is detected by the new theory as spurious, whereas former theories would have labelled it the most important.
  32. There is an 0.75 chance that any one letter in an ELS will not be a key word, so the probability that all three Hebrew letters in "Eden" are not in key words is .753 = 0.42.
  33. The probability of "Eden" intersecting itself is pc,1("Edn") = .00363 per possible ELS spacing. The chance of intersecting the second most important key word is the probability of getting all three letters correct (.0369 x .0231 x .0463) times 3 (number of letters in "Edn" any of which could be in any letter of key word), times 3 (number of letters in typical key word) equals 0.00036. Adding that to the probability of Eden intersecting itself yields .00399. Then multiply that result by 164 possible ELS spacings, times 2 for forward or backward gives an expected value of 1.31 intersections of an encoded "Eden" intersecting the very words "Garden of Eden" in the text. The Poisson estimate (see footnote 29) of the probability of finding 9 is then 1.319 exp(-1.31)/9! = 1/118,000.
  34. The probability of finding the three letters in the right places to form the mandala figure equals the chance of having an even number of letters between the two "Edens" (.5) time the chance of a daleth there (.0231) times the chance of finding another daleth that same number of spaces before the first or after the last "Eden" (2 x .0231) times the chance of finding either an ahyin or a nun at one of the two corners (.0369 + .0463) = .0000444 = 1/22,500. Then multiply that by the chance of hitting at least one key word (.58) yields 1/39,000.
  35. The probability is the chance of finding a daleth at the right place (0.0231) times find an ahyin (.0369) to complete the leg starting in "Garden" times the chance of finding either an ahyin or nun (.0369 + .0463) to complete the other leg, times 80 possible ELS spacings times 2 (forward or backward) = 1/88.
  36. The probability is that of any cross (1/88 from footnote 35) times the chance of intersecting as word as good or better than "tree" (24/329), times "knowledge" (37/329), times "
    ground" (71/329) times 6 possible permutations for those three words = 1/8,200.
  37. This is from the definition of conditional probabilities, namely, that the probability of A given that B has occurred is the probability of both A and B occurring, divided by the probability of B happening. That is really just another way of saying that any probability is the number of successes divided by the total number of possibilities.